I have a strong memory of my mother teaching me the basic idea of algebra, before we started learning it at school.
My memory is that we were in the car, stuck at a traffic light. I guess in suburban Australia, that’s the usual context for a casual conversation to pass the time. The question she asked was this. Suppose a ribbon is wrapped in a tight circle around the whole Earth. Suppose the ribbon is then lengthened by one meter, and adjusted to be an equal height above the Earth all the way around. How high is the ribbon above the ground?
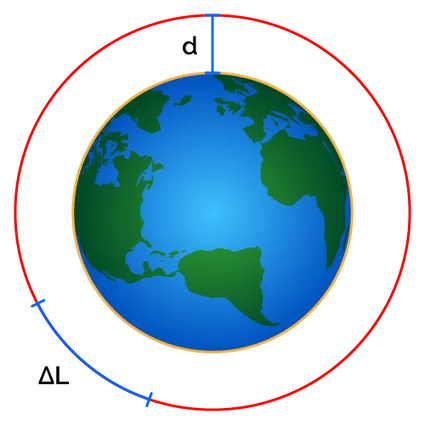
“What is the radius of the Earth?” I asked. Her answer was life-changing for me.
“This is a maths test. If the teacher didn’t put the radius of the Earth in the question, that must mean that you don’t need it. The answer is the same no matter what the radius is. So what you can do is, just make up any radius you like to make the maths easier.”
“Huh. OK, how about one meter?”
“Try zero meters.”
Well, with a radius of zero meters, the original length of the ribbon is zero meters. The new ribbon is a circle of circumference one meter. The distance above the infinitely-small Earth is the radius of that circle, which is one over pi. The end.
There are two lessons from this. The first is the basic principle of algebra: there are numbers that exist, but whose value you do not know. Nevertheless, it is possible to reason about the relationships between those numbers, and state new, true facts about those numbers, without ever needing to know their actual values. And of course with that lesson well-learned, Basic, C++, PHP and Lisp are just matters of syntax.
The second lesson is: don’t read the question. Use the question to gain insight into the mental state of the teacher. Then give the teacher what they want, and the teacher will be grateful enough to give you high marks.
This came to mind reading about the maths test question called “GSM-NoOp”:
Oliver picks 44 kiwis on Friday. Then he picks 58 kiwis on Saturday. On Sunday, he picks double the number of kiwis he picked on Friday, but five of them were a bit smaller than average. How many kiwis does Oliver have?
Of course, LLMs all say the answer is 185. They appear to have learned the second lesson, but not the first. They recognise that this is a classic maths test question. Therefore all the stated numbers must be important, otherwise why were they mentioned?
The odd thing about this is that machine learning was originally celebrated for the exact opposite ability, of stripping away unnecessary data to identify the core important factors. The Nobel Prize in chemistry was just awarded for the use of machine learning to identify proteins. This relies on the preternatural ability of machine learning to see through the mess of data that easily distracts humans. There are certain patterns, invisible to us, that allow the basic structure to be determined quite reliably. The remaining details are a second step.
The problem is that large language models were trained not to give correct answers, but to give natural language answers. Those natural language answers are judged not on how correct they are, but on how satisfying they are. And an answer to a question is always more satisfying if it incorporates all of the information in the original question.
Which is to say: I remain a skeptic concerning large language models. These are not going to revolutionise anything. But machine learning remains a powerful technology. The lesson of large language models is that within a given paradigm, machine learning really can achieve spectacular results. But it still takes a human to define the right paradigm in the first place.